Stress in Finite Element Analysis

Editor’s Note: Tony Abbey teaches live NAFEMS FEA classes in the U.S., Europe and Asia. He also teaches NAFEMS e-learning classes globally. Contact Tony at [email protected] for details.

One of the first issues when thinking about stress is defining the term. We use stress to mean something that is flowing through a structure and that we can use to compare against allowable values for strength assessment. However, it is difficult to visualize three-dimensional stress in a complex component. A typical post-processor stress selection pull-down menu might contain 30 choices, which just compounds the problem. If we are a bit hazy about what a stress really is, then what do these menu items represent? By the end of the article you should have a better idea of what some of the choices mean. A further installment will follow this article.

Understanding Forces

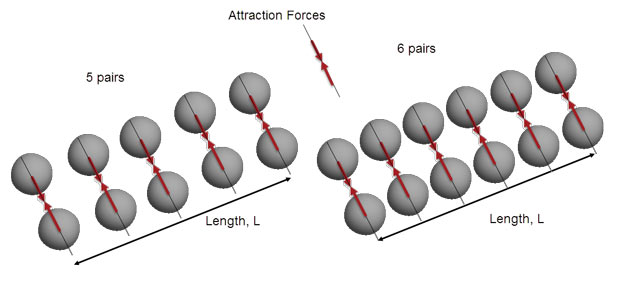
To understand stresses, it is easier to start by recapping on what we know about forces. A force is something we can sense and measure more directly. Right down at the atomic level, atoms are subject to mutual forces of attraction and repulsion. When a structure is in an unloaded condition, the atoms are in a neutral state where these forces balance. If a component is loaded externally, then the atoms are moved out of equilibrium and mutual internal forces are developed that balance the applied forces. Imagine an array of little rigid spheres connected together by springs. The springs develop a pattern of internal forces that balance the applied forces. Fig. 1 is a very crude schematic showing attractive forces developed between two instances of row pairs of atoms. The atoms are more closely spaced in one group (with six pairs) than the other (with five pairs) as shown. If each adjacent pair sees the same level of force, then one group will have a larger force developed internally over their local region: length L. We can describe the difference in the intensity of forces by using force per unit length, or in a more general sense, per unit area. In the limit as we approach small areas, this measure of intensity of the force is what we describe as stress.

Fig. 1: Attraction forces between rows of atoms stretched by external loading.

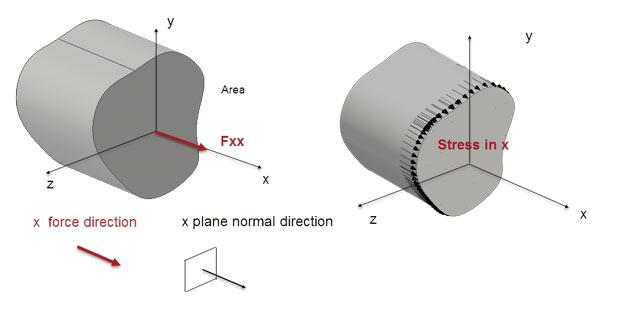
Now consider a beam-like component of arbitrary shaped cross section as shown in Fig. 2. There is a net force Fxx applied across the cut face yz in direction x. If the force is evenly distributed across the face, and there are no local constraints and the material is continuous, then the stress is constant and is given by force divided by area. The terminology for the force is Fxx, the corresponding stress is Sxx. The notation is based on defining the cut plane in which the force is acting (the first subscript x). The second subscript x indicates the direction the force is acting in. The awkward thing here is that the plane is defined by the vector that pierces it in a normal direction (x in this case).

Fig. 2: Normal force and stress definitions in the x direction and x normal plane.

The Force and Stress Cube

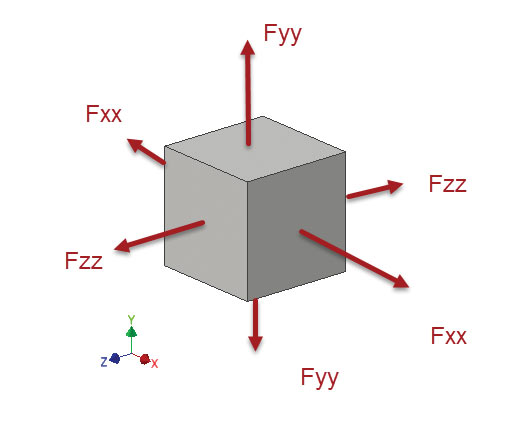
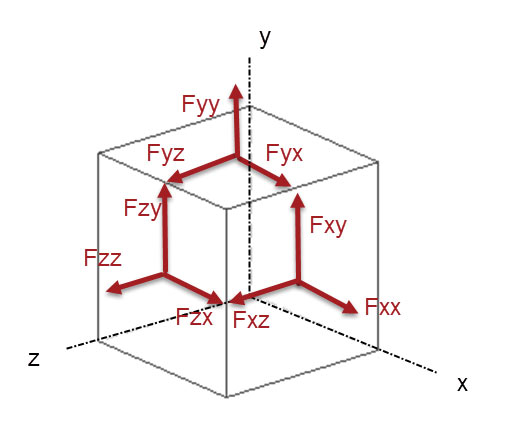
The reason for being pedantic about the indices is that we are going to extend the discussion from 1D uniaxial force and corresponding stress state to a general 3D state. This is usually done with reference to an infinitely small cube of material as shown in Fig. 3. The cube is so small that there is no variation in stress within the volume. It is all just one-stress state. Fig. 3 shows the remaining set of forces Fyy and Fzz. These are known as the normal forces that are acting normal to the respective cut faces. The force Fxx is traditionally abbreviated into just Fx. Forces Fy and Fz are treated in the same way. We will keep the full definition for now.

Fig. 3: Balanced 3D normal forces.

Normal forces result from force components acting perpendicular to the cut plane, which is why we can drop the second subscript. The other type of force is a shear force. This is not so intuitive as a normal force. Fig. 4 shows a section under a guillotining or shearing type loading. The cut face is defined by the yz plane (normal vector x). It has an external load applied, resulting in internal balancing force acting in the plane of the cut face. The applied force is a traction in the y direction. The definition of the force is Fxy; (x for the cut plane, y for the force direction). Also shown are the set of complementary internal balancing shear forces that must exist. For a cube with equal sides, the shear forces balance; Fxy = Fyx. I have tried to highlight the index lettering scheme in Fig. 4.

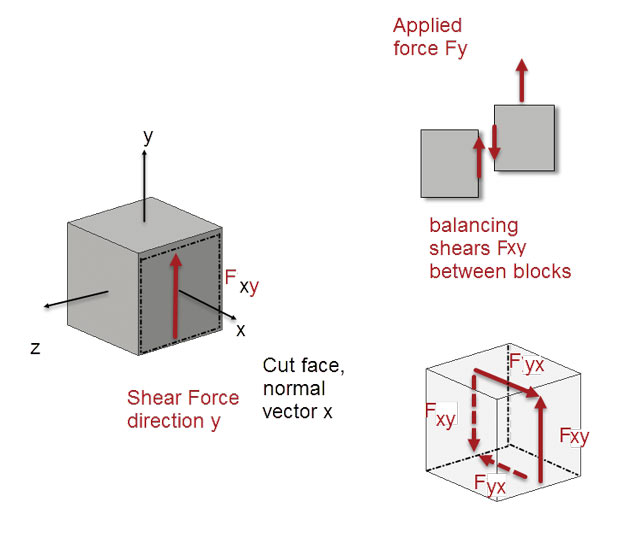Fig. 4: Shearing loading generating Fyx shear force applied to cut face. Balanced shear force system shown.

We can summarize the actions of the forces on a cube of material that is buried deep inside a component. If we pull apart two opposite faces of the cube, we develop a tensile normal force thorough the cube. If we squeeze the opposite faces, we develop a compressive force in the cube. If we apply in plane tractions to two opposite faces we develop shear forces in these faces, but also develop complementary opposing shear forces on the top and bottom faces. The complementary shear forces are puzzling at first. However, the cube must be in balance. If we only have shear forces on the front and back x vector faces, then we have a net moment. The complementary set of forces on the top and bottom y vector faces create an exactly opposite moment, and so complete the balance.

The general force situation is shown in Fig. 5. It is worth looking at the index convention to make sure it is clear (and also check my diagrams). If we imagine that the cube is small enough to have a constant force distribution on each face, then the stresses will be constant. I have used the full index notation for normal stress, so Fx is shown as Fxx. This shows the consistency in the scheme. There is a complementary set of forces on the hidden faces. I have not shown these for clarity.

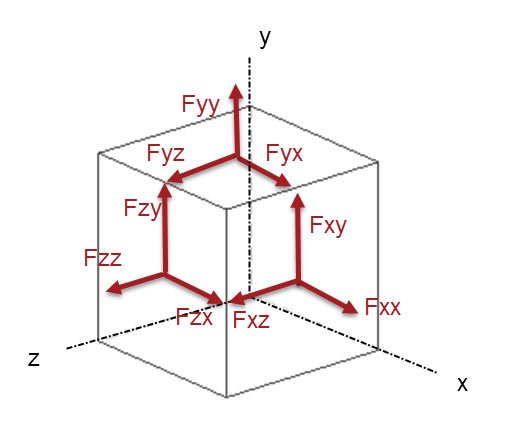Fig. 5: Full set of normal and shear forces shown on visible faces. Complementary set exists on hidden faces.

Stresses Follow Forces

I always think it is easier to imagine forces acting on an object. We could imagine setting up an FE (finite element) analysis of the cube with the loads applied externally. The transition to the corresponding general stress state is shown in Fig. 6 and it is simply force per unit area for each force vector. Some of the stress terms in a typical selection menu are now apparent. The following common terms are identified from Fig. 6:

• Solid X-Normal Stress is Sxx

• Solid Y-Normal Stress is Syy

• Solid Z-Normal Stress is Szz

• Solid XY-Shear Stress is Sxy

• Solid YZ-Shear Stress is Syz

• Solid ZX-Shear Stress is Szx

The shear indices may swap on your post-processor, as Szx = Sxz, etc. The order of the shear stresses in the menu may also change, which makes no difference to the data being selected. The normal stresses may be labeled Sxx, rather than Sx. Again these are referring to the same quantities.

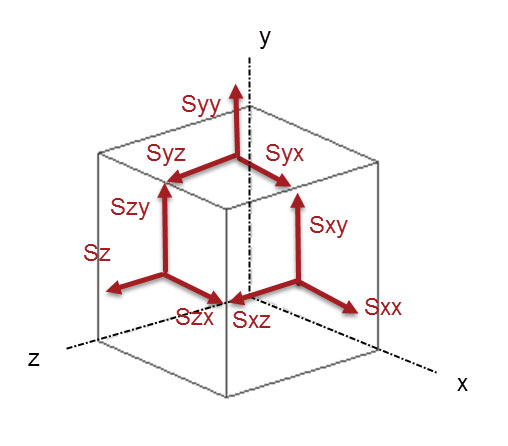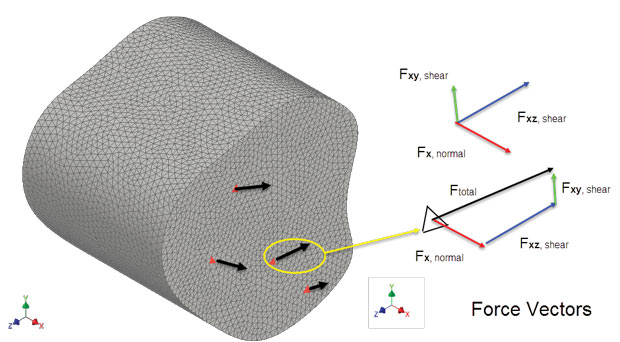
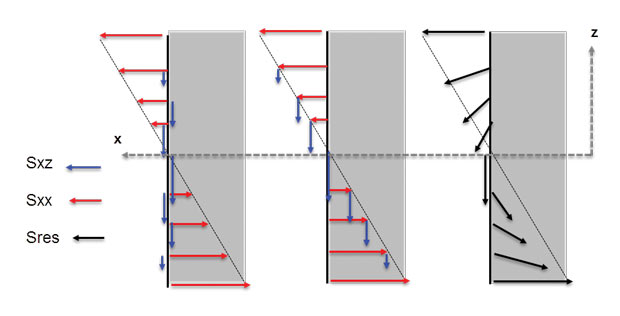
Fig. 6: Full set of normal and shear stresses shown on visible faces. Complementary set exists on hidden faces.

Fig. 7 shows the arbitrary cross-section meshed with elements. The elements represent discrete areas where we can relate the local forces to the local stresses. In a rod element, for example, there is a simple relationship between the axial force and axial stress. For a solid element it is a more subtle relationship, the stresses in an element are not constant. The force balance is also occurring at eight, 10 or a higher number of nodes, in one element. However, I have indicated some notional forces balancing each element stress distribution. The idea here is to show the forces at each element are a resultant direction and magnitude. It is easy to break down the force vector into its normal and shear components. One element is pulled out in Fig. 7 to show this. The sense of the approximate loading in that element region is clear. I think it helps to interpret the meaning of the corresponding Sxx, Sxy and Sxz stresses, which have to be plotted vector component by vector component.

Fig. 7: Force vectors at a selection of elements, with one example of vector components shown.

I find it easier to imagine forces “flowing” through the internal volume of a structure. A vector plot of this type is a complete description of the local structural load path. It is very difficult to present stress vectors in such a concise way. We will discuss principal stresses in the next installment of this article, as they come closest to this concise ideal. There have been attempts to use the force vector approach in post-processing, but the implementation seems surprisingly difficult in a general 3D sense.

One significant issue is that element nodal forces are often not very meaningful in a physical sense. Their function is more of a mathematical balancing act than engineering. It is better to integrate stress distributions locally to estimate running loads and forces.

Fig. 8 shows a 2D view of forces at the cut face of a rectangular beam section under bending and shear loading. The axial normal forces are shown, with a classic engineer’s theory of bending distribution. A parabolic shear force distribution is also shown. The shear distribution is interesting as it shows how the free surface shear force needs to be zero. No force can poke out of the top or bottom free surface. This helps visualize the same rule for shear stresses. They must be zero at the free surface.

Fig. 8: Force vectors in a beam cross section subject to bending and shear.

The Art of Load Paths

The final strength assessment is made against peak local stress levels in most cases. So understanding stresses is important. In the next installment, we will look more closely at other stress components in a typical menu selector list. I will present a methodology for plotting a logical sequence of stress types to gain fuller understanding.

However, understanding load paths is also very important – and often neglected. How does the load get into, through and out of the component? It is very much more of an art than a science to do this effectively. The force vector diagram is very helpful in understanding the corresponding stresses. I tend to make rough load path sketches by turning local stresses into equivalent force vectors. The force vectors are then used to visualize the load paths through the structure.

I believe that visualizing both forces and stresses is a useful way to keep a clearer picture of how the structure is responding under static loading conditions.