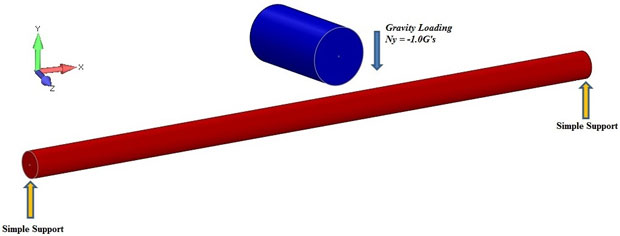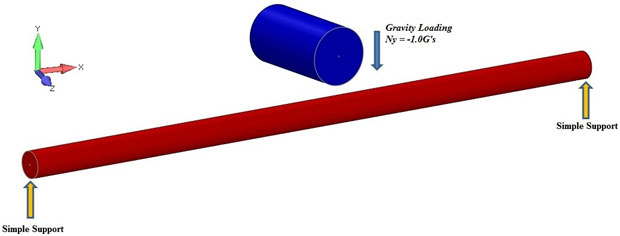
Fig. 1: Vertical Drop Impact.
Latest News
October 15, 2015
By David Dearth, P.E.
The topic of this technical article is to predict the maximum force produced due to impact when a concentrated mass is dropped from a known height and strikes a uniform beam at mid-span. In this case, the transient dynamic impact response problem is expanded to include rebound in the nonlinear, transient, dynamic impact solutions. Later I’ll expand the impact problems to include with penetration.
Introduction
When engineers are asked to address systems subjected to impact loads and nonlinear analysis tools are not available, then they are left having to take a quasi-static analysis approach. With quasi-static approaches engineers will typically assume, or apply, generous factors of safety to the static loads and then go forward with a conventional static analysis. The magnitude of the assumed factors of safety is usually left up to the discretion of the cognizant engineer in charge of the project and these factors of safety can vary greatly. A better approach would be to actually incorporate the impact loading directly into the analysis by using nonlinear transient dynamic impact response instead of simply running a conventional static analysis with some large factors applied.When an object impacts a structure, the magnitude of the impact force is often of interest and the magnitude of these impact forces can vary greatly. As an example, consider the simple impact condition where a concentrated mass is dropped from a known height and the only forces acting are gravitational acceleration. Fig. 1 shows a sketch of an impact situation where a simply supported, uniform beam is impacted by a concentrated mass. The mass is subjected to gravitational acceleration only and is dropped from a known height above the beam, impacting the beam at the mid-span.
Maximum Force Due to Impact from Dropped Mass
In many impact conditions it is desired to compute maximum force and deflections during the peak nonlinear transient response during the impact event. For this approach to the solution, maximum forces and stresses are computed by letting the impacting mass rebound (or bounce off) of the impacted beam.
Consider a simple supported uniform beam impacted by a concentrated mass. Energy methods can be used to develop an approximate solution to compute the maximum force due to impact when the concentrated mass is dropped onto the beam at the beam mid-span. The maximum force, Fmax, due to a concentrated mass W impacting a uniform beam at mid-span, from a known height, h, is the following: (Reference 1 & 2).
Sample Problem: Uniform Beam Impacted by Concentrated Mass Dropped From Known Height
Fig. 2 shows a sample problem selected to investigate nonlinear transient impact solutions. In this example, a simply supported uniform beam is impacted by a concentrated mass dropped from a known height. The only force acting on this problem is the force of gravity and the elastic restoring forces of the beam. The problem is to compute the maximum impact forces, Fmax, during the transient response of the beam during impact. For our sample problem, it is desired to estimate the peak impact force due to the impacting mass.
For this sample problem it is assumed the impacting mass can rebound or bounce back off of the beam. This sample transient problem contains all the features of any real life problem and can be found in the engineering literature in just about any texts that address impact.
To gain confidence in our solution we will present two approaches; (a.) hand solutions using conventional equations found in most engineering textbooks addressing impact problems and (b.) correlate results with a finite element idealization using Nastran FEA (finite element analysis) code.
For the Beam/Mass system shown in the Fig. 2, assume the beam length is L=24 in. and the beam cross section is a circular section d = ½ in. The concentrated mass weight, W = 5.0 lbf, is dropped from a known height, h, and impacts the mid-span of the simply supported beam. Compute maximum impact forces during the nonlinear transient response during the impact event.
When performing these transient nonlinear impact analyses, one difficulty novice FEA analysts confront is how to ensure they have performed all the necessary tasks to predict maximum deflections and stresses and to generate the correct time history response. The answer to this question can be answered by taking the time to do these sample problems. These sample FEA problems should be such that you can compute a known theoretical solution or a solution that can be validated by laboratory test data. With a sample problem and known solution, analysts can have a detailed hand sanity check that is completed using a pencil, paper and a calculator.
The perspective to keep in focus is that the same steps that analysts must jump through to solve this simple beam-mass-impact system are the same steps needed to solve the real problem using the computer. The only difference between the FEA approach and the hand solutions are usually the complexity of the geometry.
Answers
The approximate solution obtained by solving energy equations for predicting the transient response for the model shown in Fig. 2 can be found in Reference 1 and 2. This theoretical solution can be used to approximate the maximum impact force at the beam mid-span at Fmax-energy = 57.8 lbs. Fig. 3 plots the transient dynamic time history results from an FEA model idealization of Fig. 2 processed using Nastran. In Fig. 3 a 10 element FEA model solution predicts the maximum impact force Fmax-FEA= 58.1 lbs. A comparison to the theoretical energy solution gives a percent difference = ± 0.5%.
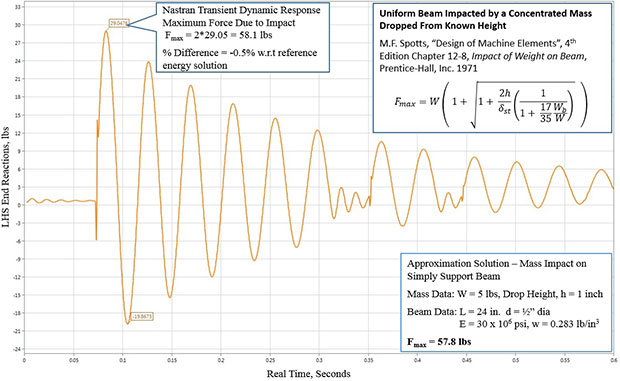 Fig. 3: Summary Results FEA Solution – Simply Supported Uniform Beam Impacted by Concentrated Mass
Fig. 3: Summary Results FEA Solution – Simply Supported Uniform Beam Impacted by Concentrated Mass-Time Dependent Response Mass Dropped from Known Height at Impact.
David Dearth, P.E., is president of Applied Analysis & Technology, located in Huntington Beach, CA. Contact him via [email protected].
Subscribe to our FREE magazine, FREE email newsletters or both!
Latest News
About the Author
DE’s editors contribute news and new product announcements to Digital Engineering.
Press releases may be sent to them via [email protected].